す角を求めるために、船体表面形状を表すパラメータとして、船体横断面船底部の傾斜角β、バウラインの傾斜角θ、水線の接線が船体中心線となす角αを用いる。この内二つが分かれば残りの一つを求めることができる。（2.1.15式）

このパラメータを用いて、衝撃角が求められる。（2.1.5式）

衝撃速度も船体の上下揺れ、縦揺れによる上下方向の速度と、船体の前進速度、波面の上下方向速度、船体表面と水面の相対的関係から求められる（2.1.6式）。

衝撃時の船体の回転の中心は船尾から1/4Lの位置にあるとしており、船体の任意の位置の船体運動による速度はこれから求められる。（2.1.7式）

（5）平均有効圧力

船体に加わる衝撃水圧は衝撃角が小さい範囲では鋭いピークを持ち、船体表面上を水面とともに高速で移動する。衝撃角が大きくなるとピーク値は下がり、圧力分布は次第にフラットになってくる。衝撃水圧を部材に作用する荷重として評価する場合に、厳密には動的な影響を考慮する必要があるが、ここでは安全側をとって、衝撃水圧の空間的な平均値で荷重として評価している。圧力分布はWagnerの理論式で与えられる。対象部材上の圧力の平均値と圧力のピーク値の比は、接水部分の大きさと部材の大きさの比に応じて計算できる。これは修正係数Fとして式で与えられている（2.1.16及び2.1.17式）。

−2.衝撃荷重発生の範囲外における衝撃荷重は、図2.2に示すように衝撃荷重が発生しうる範囲の後端位置の船底荷重をPoとした時に、Ls後端の船底荷重はPo/2とし、当該位置の船底荷重は両者の直線補間により求めた値以上とした。

−3.船底構造に作用する静的荷重として、静喫水、波浪変動荷重及び船体傾斜による付加水頭を考慮し、それらを足し合わせたものを要求値とした。

このうち、静喫水については、計画最大満載喫水を用いることとし、波浪変動荷重にっいては、一般的に有義波高（1/3最大平均値）と最大設計波高（1/1000最大期待値相当）との高さの比は、ほぼ1：2の関係があることから、基準中、2.2.1.1.に規定する有義波高（1/3最大平均値）の片振幅（波の山）の値を2倍すること（Hw/2×2＝Hw）により、最大設計波高（1/1000最大期待値相当）の片振幅（波の山）に相当する荷重を想定した。

また、船体傾斜（θ）による付加水頭（△）については、次の算式による値を想定した。

　

　

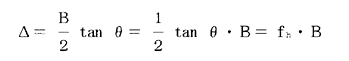
ここで、HSCコード第2章には、損傷時における船舶の許容傾斜角は、旅客船にあっては15°（通常10°）以下及び貨物船にあっては20°（通常15°）以下と規定されており、船種の応じ、それぞれ許容最大傾斜角の値を用いて次のように基準中のfhを規定した。

前ページ　　　目次へ　　　次ページ